
Keith Devlin's four levels of abstraction...plus 1:
|
|
|
|
|
|
|
|
|
|
|
|

|
|
|
| Compared with Aristotle's
concept, the energy of science has more power for making things happen
the way we want, and it is more free from arbitrary choice we might wish
to impose on it. In the universe of science and math, that makes
it "more real" than the metaphor.
But until we gain some recognition of the math-generated concept--and that takes some hard work for most of us--the metaphorical meaning seems the "more real." Our more easily-understood sense of meaning easily stands in the way of our awareness that the more abstract sense exists. The metaphor masks the meaning of the math. |
|
|
|
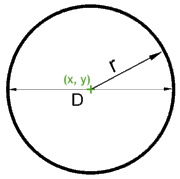
| Using letters to
represent numbers is an acquired taste. But it's also a skill, a
skill that opens the doors to the realms of mathematics. Those
parameters, spelled out as "r," "D," pr2,
and The metaphor easily masks the meaning of the math. |
QUANTUM
JUMP

|
and seldom have time to try to find effective ways to explain what a quantum jump actually is. |
|
| The metaphor masks
the meaning of the math. "Big change" is easy to understand.
However, the meaning of the Uncertainty Principle, the mathematical expression
of the quantum limit of measurement, is mired in the mathematics of physics,
which takes human thought and insight beyond human perceptions, imagination,
and metaphor. (And to many who use it, much is magic, because it
seems beyond human powers.) Furthermore, its meaning will be missed
to the extent our thinking suffers from infection with "The Singles," single
components of measurement, single-dimension (rank) ordering when we compare,
single cause and single effect, single-mindedness, etc.
The Uncertainty Principle always speaks of two measurements taken as a inseverable whole. Position and momentum. Energy and time. Angular position and angular momentum. The quantum uncertainty of one (the uncertainty of the measurement when the measuring instrument is perfectly precise) is always tied to the uncertainty of the other. The product of the two uncertainties--say of position and of momentum--is a fundamental constant of nature. How accurately we choose to measure one of the two is an arbitrary decision on our part, something like the arbitrary decision of which streets are the zero-streets for house numbers. It affects the numbers, but it doesn't affect the reality represented by the numbers. |
|
|
|
|
|||||
|
Meet "phase space." The vertical dimension represents position--in the x-direction. The horizontal direction represents momentum (velocity X mass)--in the x-direction, Px. For a particle, a point in this (blue) space represents: a value of position (x-component only) and a value of momentum (x-component only). X can vary from the value at the bottom edge of the blue to the value at the top edge--It's being held there by impenetrable walls. The value of the momentum is limited by the energy the particle has--but it will be constantly shifting that momentum from direction to direction (x, y, and z): Here we look only at the x-component. At any instant, the particle has an "uncertainty box" which might be very tall and somewhat narrow, or very wide and not tall at all, or it might be kind of square. Tall boxes represent relatively uncertain values of position and relatively certain values of momentum. Wide boxes represent more certainty in position, less in momentum. Square boxes represent balanced uncertainties. The uncertainty principle
is the observation that all the boxes have the same area no matter what
their shape. That area is 1. The total number of those boxes which can fit into this blue box is the number of different ways the particle can be in the state we are examining, the more there are the more probable that state. 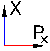 |
The calculation of entropy from the uncertatinty principle works like the calculation of the odds of rolling various values, from 2 to 12, in a single roll of a pair of dice. We count the different ways things can be that are equivalent: with the dice there is only one way to roll a 2 or a 12, and there are many ways to roll a seven. (How many ways?) Calculating entropy involves counting the many possible states that are equivalent. Before quantum mechanics we would expect the number to be infinite using such an approach. But those "uncertainty boxes" are a limit to the number of states we can distinguish between. The simplest case
for entropy is a particle confined to a box of known dimensions, and having
an energy of known value
|
|
|||||
|
|
|||||||
.
Watch for:
Exponential Growth
Epicenter